A massa específica (m ) de uma substância é a razão entre a massa (m) de uma quantidade da substância e o volume (V) correspondente:
Uma unidade muito usual para a massa específica é o g/cm3 , mas no SI a unidade é o kg/m3 . A relação entre elas é a seguinte:
Assim, para transformar uma massa específica de g/cm3 para kg/m3, devemos multiplicá-la por 1.000 . Na tabela a seguir estão relacionadas as massas específicas de algumas substâncias.
Substância | ||
Água | 1,0 | 1.000 |
Gelo | 0,92 | 920 |
Álcool | 0,79 | 790 |
Ferro | 7,8 | 7.800 |
Chumbo | 11,2 | 11.200 |
Mercúrio | 13,6 | 13.600 |
Observação
É comum encontrarmos o termo densidade (d) em lugar de massa específica (m ). Usa-se "densidade" para representar a razão entre a massa e o volume de objetos sólidos (ocos ou maciços), e "massa específica"para líquidos e substâncias.Exemplo São misturados volumes iguais de dois líquidos com massas específicas de 0,50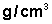 e 0,90
e 0,90 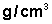 . Determine a massa específica da mistura.ResoluçãoSendo os volumes iguais, temos V1 = V2 = V . Portanto, o volume da mistura é 2V. Por outro lado, podemos dizer que a massa da mistura é igual à soma das massas dos dois líquidos. Da relação
. Determine a massa específica da mistura.ResoluçãoSendo os volumes iguais, temos V1 = V2 = V . Portanto, o volume da mistura é 2V. Por outro lado, podemos dizer que a massa da mistura é igual à soma das massas dos dois líquidos. Da relação 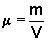 , temos
, temos 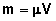 :
:

É comum encontrarmos o termo densidade (d) em lugar de massa específica (m ). Usa-se "densidade" para representar a razão entre a massa e o volume de objetos sólidos (ocos ou maciços), e "massa específica"para líquidos e substâncias.Exemplo São misturados volumes iguais de dois líquidos com massas específicas de 0,50
Fonte: Física.net

Nenhum comentário:
Postar um comentário