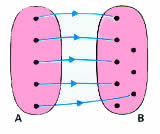
Estas são algumas propriedades que caracterizam uma função f:A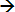 B.
B.
Função sobrejetora
Dizemos que uma função é sobrejetora se, e somente se, o seu conjunto imagem for igual ao contradomínio, isto é, se Im=B. Em outras palavras, não pode sobrar elementos no conjunto B sem receber flechas. Exemplo:
Função injetora
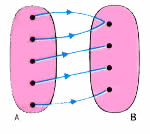
A função é injetora se elementos distintos do domínio tiverem imagens distintas, ou seja, dois elementos não podem ter a mesma imagem. Portanto, não pode haver nenhum elemento no conjunto B que receba duas flechas. Exemplo:
Por exemplo, a função f:IR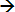 IR definida por f(x)=3x é injetora, pois se x1
IR definida por f(x)=3x é injetora, pois se x1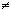 x2 então 3x1
x2 então 3x1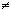 3x2, portanto f(x1)
3x2, portanto f(x1)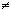 f(x2).
f(x2).
Função bijetora
Uma função é bijetora quando ela é sobrejetora e injetora ao mesmo tempo. Por exemplo, a função f: IR IR definida por y=3x é injetora, como vimos no exemplo anterior. Ela também é sobrejetora, pois Im=B=IR. Logo, esta função é bijetora.
IR definida por y=3x é injetora, como vimos no exemplo anterior. Ela também é sobrejetora, pois Im=B=IR. Logo, esta função é bijetora.
Já a função f: IN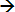 IN definida por y=x+5 não é sobrejetora, pois Im={5,6,7,8,...} e o contradomínio CD=IN, mas é injetora, já que valores diferentes de x têm imagens distintas. Então essa função não é bijetora.
IN definida por y=x+5 não é sobrejetora, pois Im={5,6,7,8,...} e o contradomínio CD=IN, mas é injetora, já que valores diferentes de x têm imagens distintas. Então essa função não é bijetora.
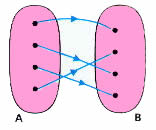
Resumindo, observe os diagramas abaixo:
 |
|
 |
|
 |
|
Fonte: Só Matemática

Nenhum comentário:
Postar um comentário