Determinantes

A toda matriz quadrada A = (a_ij)_mxn de elementos reais de ordem n está associado um único número real chamado determinante da matriz A. 

Representação 

O determinante da matriz A pode ser representado por: 



Regras Práticas 

Para o cálculo de determinantes de ordem n (n 3), procede-se da seguinte forma: 

Determinante de ordem 1 

Para a matriz A = [a₁₁] o determinante é o próprio elemento a₁1. Det A = a₁₁ 

Determinante de ordem 2 

Para a matriz    

Para a matriz o determinante é igual à diferença entre o produto dos elementos da diagonal principal e o produto dos elementos da diagonal secundária. 

Det    

-a₁₂ . a₂₁ ................+a₁₁ . a₂₂ 

det A = a₁₁a₂₂ - a₁₂a₂₁ 

Determinante de ordem 3 

Para a matriz de 3ª ordem 



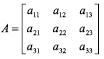
define-se: 

det A = a₁₁a₂₂a₃₃ + a₁₂a₂₃a₃₁ + a₁₃a₂₁a₃₂ - a₁₃a₂₂a₃₁ - a₁₁a₂₃a₃₂ - a₁₂a₂₁a₃₃ 

Regra de Sarrus 

Para calcular o determinante de uma matriz de ordem 3: 

Repetem-se, à direita da matriz, as duas primeiras colunas. Acompanhando as flechas em diagonal, multiplicam-se os elementos entre si, associando-lhes o sinal indicado. 

Somam-se algebricamente os produtos obtidos, calculando-se, assim, o valor do determinante.

Fonte: Colégio Web