Uma função afim, também conhecida como função polinomial de grau 1 ou função polinomial de primeiro grau é uma função do tipo cujo gráfico é uma reta não perpendicular ao eixo Tal função também pode ser entendida como uma transformação linear () seguida por uma translação ().
no caso finito-dimensional cada função afim é dada por uma matriz A e por um vetor B, que possam ser escritos como a matriz A com uma coluna extra do B. Fisicamente, uma função afim é a que preserva:
- Colinearidade entre pontos, isto é, três pontos que se encontram em uma linha continuam a ser colineares após a transformação;
- relações das distâncias ao longo de uma linha, isto é, para os pontos colineares distintos ,
Uma função afim é composta de um ou de diversos transformadores lineares. Diversas transformações lineares podem ser combinadas em uma única matriz, assim que a fórmula geral dada acima é ainda aplicável.
Em uma dimensão (ou seja, quando x e y são escalares), os termos A e b são chamados, respectivamente, de coeficiente angular e coeficiente linear.
Definição Formal
Uma função chama-se função afim quando existe dois números reais e tal que e para todo
Coeficientes
Para facilitar a análise dessas funções, dizemos que o coeficiente "a" da função é o coeficiente angular ou declividade da reta. Esse coeficiente determina a inclinação da reta que representa a função.
O coeficiente "b" determina o deslocamento da reta em relação à origem, por isso ele é conhecido como coeficiente linear da reta.
Função Linear
Uma função linear é um caso particular da função afim onde e sendo, portanto, expressa como:
Veja na figura abaixo um exemplo de gráfico de função linear.
| Esboço do gráfico da função f(x)=2x, um exemplo de função linear |
Um caso específico da função linear é a função identidade, onde Logo a função identidade é expressa como:
Observe na figura abaixo um exemplo de gráfico de função identidade.
 |
| Esboço do gráfico da função f(x)=x, a função identidade |
Função Linear e Proporcionalidade
Uma das principais aplicações da função linear é a relação de proporção existente entre os elementos do domínio e da imagem, pois observamos que conforme variam os elementos do domínio, suas respectivas imagens variam na mesma proporção, sendo essa proporção o coeficiente angular da função, nesse caso chamado de taxa de variação.
Assim, seja a função linear vemos que o conjunto dos pontos que representa a reta dessa função são os pontos do tipo onde é a razão entre e
Essa relação será diretamente proporcional se a função for crescente e inversamente proporcional se a função for decrescente.
Crescimento e Decrescimento
Uma função afim pode ser crescente, decrescente, dependendo do valor do coeficiente angular. Uma função pode ainda ser constante, se a=0 e aí ela terá grau 0.
Uma função afim é crescente quando seu coeficiente angular for positivo, ou seja,
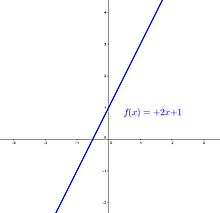 |
| Esboço do gráfico da função f(x)=2x+1, um exemplo de função afim crescente |
Uma função afim é decrescente quando seu coeficiente angular for negativo,ou seja,
 |
| Esboço do gráfico da função afim f(x)=-2x+1, um exemplo de função afim decrescente. |
Uma função é constante (neste caso dizemos que ela não é afim) quando seu coeficiente angular for nulo, ou seja Nesse caso a equação que define a função é dada por e seu gráfico é uma reta paralela ao eixo
 |
| Esboço do gráfico da função f(x)=2, um exemplo de função constante |
Zero
O zero de uma função afim (ou raízes da função) é o valor de para o qual a função é igual a zero. Geometricamente o zero de uma função afim é o ponto de corte no eixo das abcissas.
Para definir este ponto basta resolver a equação
Logo o ponto de corte no eixo das abcissas é
Toda e qualquer função afim também corta o eixo das ordenadas (eixo ). Para definir este ponto de corte basta calcular
Logo o ponto de corte no eixo y é
 |
| Pontos de corte com os eixos em uma função afim |
Fonte: Wikipédia




































Nenhum comentário:
Postar um comentário