Sabemos calcular o inverso de um número real e o inverso de uma matriz segue o mesmo conceito. Quando queremos encontrar o inverso de um número real temos que nos orientar pela seguinte definição:
Sendo t e g dois números reais, t será inverso de g, se somente se, t . g ou g . t for igual a 1.
Quando um número real é inverso do outro, indicamos o inverso com um expoente -1:
1 / 5 = 5-1, dizemos que 1 /5 é o inverso de 5, pois se multiplicarmos 1 / 5 . 5 = 1
Dizemos que uma matriz terá uma matriz inversa se for quadrada e se o produto das duas matrizes for igual a uma matriz identidade quadrada de mesma ordem das outras.
Dada duas matrizes quadradas C e D, C será inversa de D se, somente se, C . D ou D . C for igual a In. Portanto, dizemos que
C = D-1 ou D = C-1.
Exemplo 1:
Verifique se a matriz A =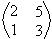 e a matriz B =
e a matriz B = 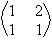 são inversas entre si.
são inversas entre si.
Para que seja verdade o produto A . B = I2.
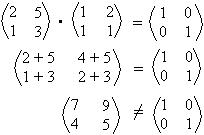
Portanto, concluímos que as matrizes A e B não são inversas.
Exemplo 2:
Verifique se as matrizes G= e K=
e K= 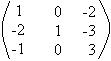 são inversas entre si.
são inversas entre si.
Para que seja verdade o produto de G . K = I3
Sendo t e g dois números reais, t será inverso de g, se somente se, t . g ou g . t for igual a 1.
Quando um número real é inverso do outro, indicamos o inverso com um expoente -1:
1 / 5 = 5-1, dizemos que 1 /5 é o inverso de 5, pois se multiplicarmos 1 / 5 . 5 = 1
Dizemos que uma matriz terá uma matriz inversa se for quadrada e se o produto das duas matrizes for igual a uma matriz identidade quadrada de mesma ordem das outras.
Dada duas matrizes quadradas C e D, C será inversa de D se, somente se, C . D ou D . C for igual a In. Portanto, dizemos que
C = D-1 ou D = C-1.
Exemplo 1:
Verifique se a matriz A =
Para que seja verdade o produto A . B = I2.
Portanto, concluímos que as matrizes A e B não são inversas.
Exemplo 2:
Verifique se as matrizes G=
Para que seja verdade o produto de G . K = I3
Portanto, concluímos que as matrizes G e K são inversas entre si.
Fonte: Brasil Escola
Por Danielle de Miranda
Graduada em Matemática
Graduada em Matemática


Nenhum comentário:
Postar um comentário