Grandezas Angulares
As grandezas até agora utilizadas de deslocamento/espaço (s, h, x, y), de velocidade (v) e de aceleração (a), eram úteis quando o objetivo era descrever movimentos lineares, mas na análise de movimentos circulares, devemos introduzir novas grandezas, que são chamadas grandezas angulares, medidas sempre em radianos. São elas:
- deslocamento/espaço angular: φ (phi)
- velocidade angular: ω (ômega)
- aceleração angular: α (alpha)
Saiba mais... Da definição de radiano temos:   Desta definição é possível obter a relação:  E também é possível saber que o arco correspondente a 1rad é o ângulo formado quando seu arco S tem o mesmo comprimento do raio R. |
Espaço Angular (φ)
Chama-se espaço angular o espaço do arco formado, quando um móvel encontra-se a uma abertura de ângulo φ qualquer em relação ao ponto denominado origem.
E é calculado por: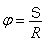
Deslocamento angular (Δφ)
Assim como para o deslocamento linear, temos um deslocamento angular se calcularmos a diferença entre a posição angular final e a posição angular inicial:
Sendo:
Por convenção:
No sentido anti-horário o deslocamento angular é positivo.
No sentido horário o deslocamento angular é negativo.
Velocidade Angular (ω)
Análogo à velocidade linear, podemos definir a velocidade angular média, como a razão entre o deslocamento angular pelo intervalo de tempo do movimento:
Sua unidade no Sistema Internacional é: rad/s
Sendo também encontradas: rpm, rev/min, rev/s.
Também é possível definir a velocidade angular instantânea como o limite da velocidade angular média quando o intervalo de tempo tender a zero:
Aceleração Angular (α)
Seguindo a mesma analogia utilizada para a velocidade angular, definimos aceleração angular médiacomo:
Algumas relações importantes
Através da definição de radiano dada anteriormente temos que:
mas se isolarmos S:
derivando esta igualdade em ambos os lados em função do tempo obteremos:
mas a derivada da Posição em função do tempo é igual a velocidade linear e a derivada da Posição Angular em função do tempo é igual a velocidade angular, logo:
onde podemos novamente derivar a igualdade em função do tempo e obteremos:
mas a derivada da velocidade linear em função do tempo é igual a aceleração linear, que no movimento circular é tangente à trajetória, e a derivada da velocidade angular em função do tempo é igual a aceleração angular, então:
Então:
Linear | Angular | |
S | = | φR |
v | = | ωR |
a | = | αR |
Período e Frequência
Período (T) é o intervalo de tempo mínimo para que um fenômeno ciclico se repita. Sua unidade é a unidade de tempo (segundo, minuto, hora...)
Frequência(f) é o número de vezes que um fenômeno ocorre em certa unidade de tempo. Sua unidade mais comum é Hertz (1Hz=1/s) sendo também encontradas kHz, MHz e rpm. No movimento circular a frequência equivale ao número de rotações por segundo sendo equivalente a velocidade angular.
Para converter rotações por segundo para rad/s:
sabendo que 1rotação = 2πrad,
Movimento Circular Uniforme
Um corpo está em Movimento Curvilíneo Uniforme, se sua trajetória for descrita por um círculo com um "eixo de rotação" a uma distância R, e sua velocidade for constante, ou seja, a mesma em todos os pontos do percurso.
No cotidiano, observamos muitos exemplos de MCU, como uma roda gigante, um carrossel ou as pás de um ventilador girando.
Embora a velocidade linear seja constante, ela sofre mudança de direção e sentido, logo existe uma aceleração, mas como esta aceleração não influencia no módulo da velocidade, chamamos deAceleração Centrípeta.
Esta aceleração é relacionada com a velocidade angular da seguinte forma:
Sabendo que 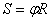e que , pode-se converter a função horária do espaço linear para o espaço angular:
e que 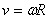, pode-se converter a função horária do espaço linear para o espaço angular:
então:
Nenhum comentário:
Postar um comentário