Vamos analisar um exemplo para entender o que é uma função composta. Consideremos os conjuntos:
A={-2,-1,0,1,2}
B={-2,1,4,7,10}
C={3,0,15,48,99}
B={-2,1,4,7,10}
C={3,0,15,48,99}
E as funções:
f:A B definida por f(x)=3x+4
B definida por f(x)=3x+4
g:B C definida por g(y)=y2-1
C definida por g(y)=y2-1
f:A
g:B
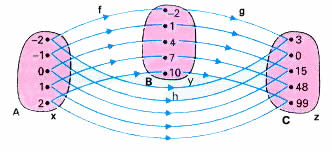
Como nos mostra o diagrama acima, para todo x 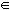 A temos um único y
A temos um único y 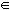 B tal que y=3x+4, e para todo y
B tal que y=3x+4, e para todo y 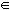 B existe um único z
B existe um único z 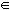 C tal que z=y2-1. Então, concluímos que existe uma função h de A em C, definida por h(x)=z ou h(x)=9x2+24x+15, pois:
C tal que z=y2-1. Então, concluímos que existe uma função h de A em C, definida por h(x)=z ou h(x)=9x2+24x+15, pois:
h(x)=z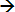 h(x)= y2-1
h(x)= y2-1
h(x)=z
E sendo y=3x+4, então h(x)=(3x+4)2-1
A função h(x) é chamada função composta de g com f. Podemos indicá-la por g o f(lemos “g composta com f”) ou g[f(x)] (lemos “g de f de x”). Vamos ver alguns exercícios para entender melhor a ideia de função composta.
Exercícios resolvidos
1) Dadas as funções f(x)=x2-1 e g(x)=2x, calcule f[g(x)] e g[f(x)].
Resolução:
f[g(x)] = f(2x) = (2x)2-1 = 4x2-1
g[f(x)] = g(x2-1) = 2(x2-1) = 2x2-2
2) Dadas as funções f(x)=5x e f[g(x)]=3x+2, calcule g(x).
Resolução:
Como f(x)=5x, então f[g(x)]= 5.g(x).
Porém, f[g(x)]=3x+2, logo:
5.g(x)=3x+2, e daí g(x)=(3x+2)/5
3) Dadas as funções f(x)=x2+1 e g(x)=3x-4, determine f[g(3)].
Resolução: g(3)=3.3-4=5
Fonte: Só Matemática

Nenhum comentário:
Postar um comentário