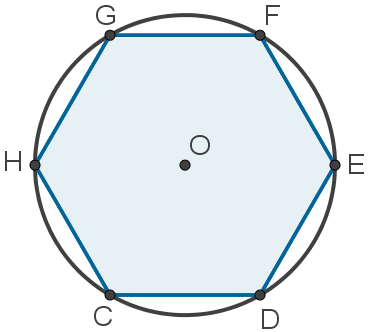
Polígonos inscritos são aqueles que estão no interior de uma circunferência, de modo que todos os seus vértices são pontos dela. Já os polígonos circunscritos estão no exterior de uma circunferência e apresentam todos os seus lados tangentes a ela. Observe as seguintes imagens:
Veja que todos os vértices do hexágono acima também são pontos pertencentes à circunferência ao seu redor. É nessa situação que dizemos que o hexágono é inscrito na circunferência ou que a circunferência circunscreve o polígono.
Nessa segunda imagem, é o polígono que circunscreve a circunferência. Também podemos dizer, nesse caso, que a circunferência está inscrita no polígono. Observe que, para isso, todos os lados do polígono são tangentes à circunferência.
Elementos do polígono regular inscrito
Centro do polígono regular
É o centro da circunferência onde esse polígono está inscrito. Pode ser encontrado a partir do ponto de encontro entre duas mediatrizes de lados distintos do polígono.
Raio do polígono regular
É o elemento que parte do centro de um polígono regular até um de seus vértices e tem a mesma medida do raio da circunferência na qual o polígono regular está inscrito.
Apótema
É o segmento de reta que liga o centro de um polígono regular ao ponto médio de um de seus lados. A apótema sempre forma um ângulo reto com o lado do polígono que ela toca.

Exemplo de centro, raio e apótema do polígono regular
Nessa imagem, r é o raio do polígono regular inscrito, o ponto O é seu centro e o segmento a é apótema.
Propriedades
As propriedades a seguir são válidas apenas para polígonos regulares, isto é, polígonos que possuem todos os lados com a mesma medida e todos os ângulos congruentes.
1 – Todo polígono regular pode ser inscrito em uma circunferência;
2 – Todo polígono regular pode ser circunscrito em uma circunferência;
3 – As mediatrizes dos lados de um polígono regular encontram-se no centro da circunferência que o circunscreve;
Em outras palavras, se um polígono regular está inscrito em uma circunferência, as mediatrizes de seus lados encontram-se no centro da circunferência, também chamado centro do polígono inscrito. A imagem a seguir ilustra essa situação:
4 – Em um polígono regular inscrito em uma circunferência, todos os ângulos centrais, cujos lados são formados por dois raios consecutivos do polígono regular inscrito, são congruentes. Além disso, é possível determinar sua medida dividindo 360° pelo número de lados do polígono.

Ângulo cujos lados são raios consecutivos do polígono regular inscrito
Autor: Luiz Paulo Moreira - Graduado em Matemática
Fonte: Escola Kids