Funções - Conceito

O que é uma função?

O conceito de função é um dos mais importantes em toda a matemática. O conceito básico é o seguinte: toda vez que temos dois conjuntos e algum tipo de associação entre eles, que faça corresponder a todo elemento do primeiro conjunto um único elemento do segundo, ocorre uma função.

O uso de funções pode ser encontrado em diversos assuntos. Por exemplo, na tabela de preços de uma loja, a cada produto corresponde um determinado preço. Outro exemplo seria o preço a ser pago numa conta de luz, que depende da quantidade de energia consumida. Observe, por exemplo, o diagrama das relações abaixo:

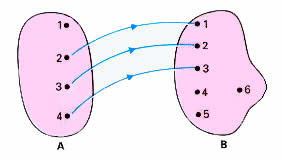
A relação acima não é uma função, pois existe o elemento 1 no conjunto A, que não está associado a nenhum elemento do conjunto B. Vamos ver outro caso:

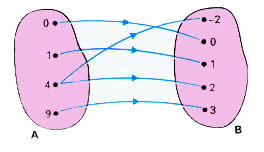
A relação acima também não é uma função, pois existe o elemento 4 no conjunto A, que está associado a mais de um elemento do conjunto B. Agora preste atenção no próximo exemplo:

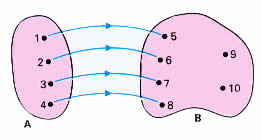
A relação acima é uma função, pois todo elemento do conjunto A está associado a somente um elemento do conjunto B.

De um modo geral, dados dois conjuntos A e B, e uma relação entre eles, dizemos que essa relação é uma função de A em B se e somente se, para todo x 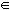 A existe um único y  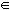B de modo que x se relacione com y.

Fonte: Só Matemática